likelihood ?
It’s very confusing concept to me, very difficult to understand at a glance. I’ve looked for the definition from Wikipedia and sought some blogs which explained about it. First of all I’ve referred sw4r ‘s blog which contained huge amount of numerical statistics. And I found the definition of ‘Likelihood’ in Wikipedia which was really helpful to me to understand meaning and usage. Also I found some helpful example in plasticcode ‘s blog.
Let’s begin to look at the definition of likelihood inside Wikipedia.
In frequentist inference, a likelihood function (often simply the likelihood) is a function of the parameters of a statistical model, given specific observed data. Likelihood functions play a key role in frequentist inference, especially methods of estimating a parameter from a set of statistics. In informal contexts, “likelihood” is often used as a synonym for “probability“. In mathematical statistics, the two terms have different meanings. Probability in this mathematical context describes the plausibility of a random outcome, given a model parameter value, without reference to any observed data. Likelihood describes the plausibility of a model parameter value, given specific observed data.
Probability and Likelihood can be opposite meaning. The probability is a function of random variable X knowing population’s parameters , while Likelihood is a function of parameter \theta when observations are measured.
The probability density function is expressed with random variable X given parameter \theta ,
f(X|\theta)
Meanwhile Likelihood is expressed with \theta given X
L(\theta|X)
In normal if there are n samples, Likelihood is written by L(\theta|x_1,x_2,\cdots,x_n)
Usually it is assumed that observations can be randomly selected and even individually independent so that it can be expressed by a multiplication.
L(\theta|x_1,x_2,\cdots,x_n)=L(\theta|x_1) \times L(\theta|x_2) \times \cdots \times L(\theta|x_n)
Let’s see an example from plasticcode ‘s blog.
Q : If we assume that 5 samples (-1, -0.5, 0, +0.5, +1) are followed to normal distribution, what is the its mean and standard deviation ?
A : To get the population’s parameters \mu and \sigma , we can try several likelihood and compare the results each other. If a result has the biggest value compared to others, we can say it can be a maximum likelihood approximately and explain the population’s parameters finely.
I’ve written somewhat R Code. You can find the R Code in Github.
1. When its distribution is assumed to N(-1, 1), likelihood is calculated by ‘0.0002376545’ (This is the simple multiplication from the 5 values in the curve.)
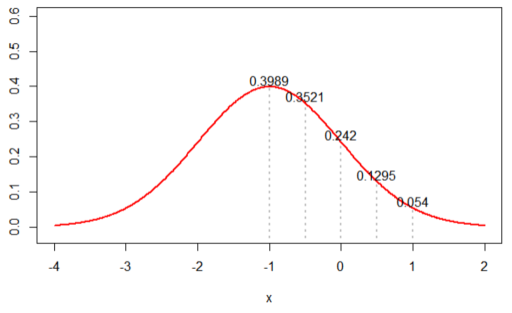
2. When its distribution is assumed to N(0, 1), likelihood is calculated by ‘0.002895224’
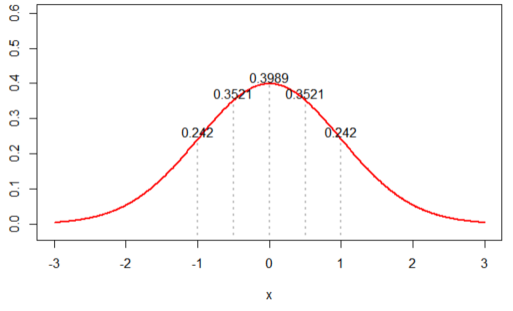
3. When its distribution is assumed to N(3, 1), likelihood is calculated by ‘4.898424e-13’ (extreme case)
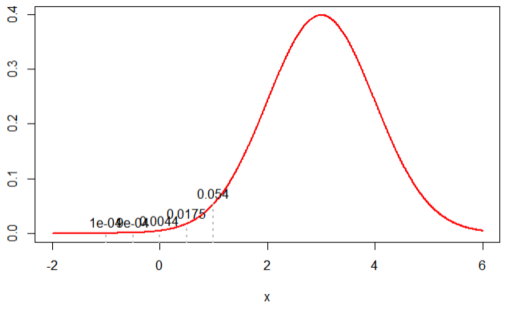
i.e. When we assumed its distribution was N(0, 1) , the likelihood was the highest. When we decide the best population’s parameters with this restricted sample counts (5), it is very accountable for. Like this, Likelihood can be estimated differently from the different samples.
I would like to recommend a funny video, titled by “probability vs likelihood” which is the best simply described the concept of likelihood.
