- 추정 (Estimation) – 개요 (Introduction)
- 추정 (Estimation) – 점 추정량의 편향과 MSE (Mean Square Error)
- 추정 (Estimation) – 일반적인 불편(unbiased) 점 추정량
- 추정 (Estimation) – 점 추정량의 적합성 산출
- 추정 (Estimation) – 신뢰구간 (Confidence Intervals)
- 추정 (Estimation) – 다 표본 신뢰구간
- 추정 (Estimation) – 표본 크기 선택
- 추정 (Estimation) – 소(小) 표본 신뢰구간 ; μ 와 μ1 – μ2
- 추정 (Estimation) – 모분산에 대한 신뢰구간
이번 포스트는 추정(Estimation) 의 다섯 번째 포스트로 신뢰구간 (Confidence Intervals) 을 다룬다. 내용은『Mathematical Statistics with Applications, Sixth Edition, DUXBURY , Dennis D. Wackerly / William Mendenhall / Richard L. Scheaffer』 를 참고했다.
5. 신뢰구간 (Confidence Intervals)
구간 추정량은 표본 관측치를 사용하여 구간의 양 끝단의 두 숫자를 계산하는 방식을 규정하는 것이다. 결과 구간은 이상적으로 두 가지 속성을 가진다. : 첫 째, 그 구간은 목적 파라미터 (target parameter) θ 를 포함한다. 둘 째, 상대적으로 좁은 구간이다. 표본의 함수식인 구간 값은 표본에 따라 변화 한다 (한 쪽 끝 또는 양 쪽 모두). 따라서 구간의 길이와 위치는 랜덤한 양이며, 특정 표본으로 부터 산출된 해당 구간안에 목적 파라미터 θ 가 들어갈지 알 수 없다. 이것을 고려할 때 우리 목표는 목적 파라미터 θ 를 높은 확률로 포함시키는 좁은 구간을 생성할 수 있는 구간 추정량을 찾는 것이다.
일반적으로 구간 추정량 (interval estimators) 을 신뢰 구간 (confidence intervals) 이라고 부른다. 신뢰 구간의 우측과 좌측 끝 점을 우측 신뢰 한계 (upper confidence limit), 좌측 신뢰 한계 (lower confidence limit) 으로 지칭한다. 신뢰구간이 파라미터 θ 를 포함할 확률을 신뢰 계수 (confidence coefficient) 라고 한다. 실제적인 관점에서, 신뢰계수는 표본 추출 (sampling) 을 여러 번 반복해서 얻어지는 신뢰구간이 파라미터 θ 를 포함하는 횟수의 비율이 된다. 만약 우리가 어떤 추정량에 해당하는 신뢰 계수가 높다는 것을 안다면, 특정 표본으로부터 구해진 신뢰구간은 파라미터 θ 를 포함할 것이라는 것을 확신 (confident) 할 수 있다.
\hat{\theta}_L 와 \hat{\theta}_U 를 각각 θ에 대한 (랜덤한) 하한, 상한 신뢰 한계라고 하자. 그러면 만약
P(\hat{\theta}_L \leq \theta \leq \hat{\theta}_U) = 1 - \alpha
라고 하면 (1-α) 확률 값은 신뢰계수 (confidence coefficient)이다. 이때 결과의 랜덤 구간 [\hat{\theta}_L ,\hat{\theta}_U] 를 양측 신뢰 구간 (two-sided confidence interval) 이라 한다.
P(\hat{\theta}_L \leq \theta) = 1-\alpha
의 확률을 갖는 단측 신뢰구간 (one-sided confidence interval) 도 표현할 수 있는데, 비록 \hat{\theta}_L 이 랜덤인 경우지만, 신뢰구간은 [ \hat{\theta}_L , \infty ] 가 된다. 마찬가지로,
P(\theta \leq \hat{\theta}_U) = 1-\alpha
의 단측 상한 신뢰 구간은 [-\infty,\hat{\theta}_U] 가 된다.
신뢰구간을 찾는 아주 유용한 한 가지 방법이 있는데 ‘피보탈 방법 (pivotal method)’ 라 지칭한다. 이 방식은 다음 두 가지 특성을 갖는 피보탈 양을 찾는 것이다.
1. 관측 값과 알려지지 않은 모 파라미터 θ 로 구성된 함수이다. (단, θ 만 unknown 이다.)
2. 이것의 확률분포는 파라미터 θ 에 종속적이지 않다.
피보탈 양이 알려져 있다면, 원하는 추정 구간을 생성하는데 다음과 같은 로직을 적용시킬 수 있다. 만약 Y 가 랜덤 변수이고 c > 0 이 상수이고 P(a ≤ Y ≤ b) = 0.7 이면, P(ca ≤ cY ≤ cb) = 0.7 을 만족한다. 마찬가지로 상수 d 에 대해서 P (a + d ≤ Y + d ≤ b + d) = 0.7 을 만족한다. 즉 P(a ≤ Y ≤ b) = 0.7 라는 확률에 Y 값의 스케일 변경이나 이동은 영향을 미치지 않는다. 그러므로 우리가 피보탈 양에 대한 확률분포를 알고 있다면, 이러한 연산을 통해서 추정 구간을 생성할 수 있다. 이 방법을 다음 예제들에서 확인 해 보자.
| 예제 1.
평균이 θ인 지수분포에서 단일 관측 값 Y 를 얻고자 한다고 가정하자. Y 를 이용하여 θ 에 대한 신뢰구간을 생성하라. (신뢰계수 = 0.90) |
풀이.
Y 에 대한 확률 분포 함수는 다음과 같이 주어진다.
f(y)=\begin{cases}\Big(\dfrac{1}{\theta}\Big)e^{-y/\theta},~y \geq 0\\0,~~~~~~~~~~~~~~~elsewhere.\end{cases}
이 책 6장에 나오는 변환 방법을 사용하면 (이 책 297 페이지에 공식이 나와 있다.), U = Y/\theta 는 다음과 같은 지수 밀도 함수를 갖는다.
f_U(u) =\begin{cases}e^{-u},~~~~~u>0\\0,~~~~~~~~~elsewhere. \end{cases}
U 의 밀도함수는 아래 그림과 같다.
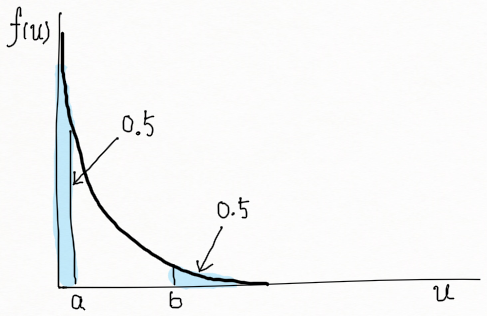
U = Y/\theta 는 Y (표본 관측결과) 의 함수이며 U의 분포는 θ 에 영향받지 않는다. 따라서 U = Y/\theta 는 피보탈 양이라고 할 수 있다. 왜냐하면 신뢰계수 0.9에 해당하는 신뢰구간을 추정하고자 하기 때문에
P(a \leq U \leq b) = 0.9을 만족하는 a 와 b 를 구해야 한다. 한 가지 방법은 a보다 작은 영역과 b보다 큰 영역이 각각 0.05 의 확률을 갖게 하는 것이다. 즉,
P(U < a) = \huge\int^{\normalsize a}_{\normalsize 0} \normalsize e^{-u}du=0.05 이며 P(U > b) = \huge\int^{\normalsize \infty}_{\normalsize b} \normalsize e^{-u}du=0.05
계산하면,
1-e^{-a}=0.05 ~and~ e^{-b}=0.05 이며, a = 0.051, b = 2.996 을 얻는다.
정리하면 다음과 같다.
0.90 = P(0.051 \leq U \leq 2.996) = P(0.051 \leq \dfrac{Y}{\theta} \leq 2.996).
θ에 대한 구간 추정양을 구하고 있기 때문에 θ 를 중심으로 하여 부등식을 다시 정리해 보자. Y 가 지수분포를 따르면 P(Y >0) =1 이므로, 양변을 Y로 나눠도 부등호는 변하지 않는다.
0.90 =P(0.051 \leq \dfrac{Y}{\theta} \leq 2.996) = P(\dfrac{0.51}{Y} \leq \dfrac{1}{\theta}\leq \dfrac{2.996}{Y}).
역을 취하면 (부등호의 방향이 바뀐다.)
0.90 =P(\dfrac{Y}{0.051} \geq \theta \geq \dfrac{Y}{2.996})=P(\dfrac{Y}{2.996} \leq \theta \leq \dfrac{Y}{0.051}).
를 얻는다. 따라서 Y/2.996 과 Y/0.051 이 우리가 원하는 하한과 상한 신뢰한계 값이다. 숫자 값을 얻기 위해서는 Y의 실제 값을 관측해야만 한다. 한계 구간이 (Y/2.996, Y/0.051) 로 생성되었고 이것은 해당 지수분포를 따라 반복적으로 표본추출하여 얻은 Y 값 (관측값) 들로부터 θ의 실제(unknown) 값이 해당 구간에 속할 확률이 90% 임을 말해준다.
| 예제2.
표본 크기가 1인 [0, θ] 구간으로 정의되는(θ는 unknown) uniform 분포에서 표본을 취한하고 가정해 보자. 95%의 하한 신뢰 한계 값을 구하라. |
풀이.
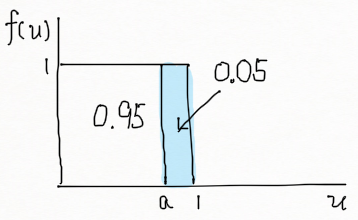
Y 는 [0, θ] 구간에서 uniform 이므로 이 책의 6장에서 보인것 처럼, U=Y/θ 가 [0,1] 구간에서 uniform 분포를 갖는다는 것을 알고 있다. 즉,
f_U(u)=\begin{cases}1,~~~~0 \leq u \leq 1\\0,~~~~elsewhere. \end{cases}
위 그림은 U에 대한 밀도함수를 표현하고 있다. U 가 예제1. 에서와 같이 피보탈 양의 특성을 만족하는 것을 알 수 있다. θ에 대한 95%의 하한 신뢰한계를 구하고자 하므로, P(U ≤ a) = 0.95 를 만족하는 a 를 구하면 된다. 즉,
\huge\int^{\normalsize a}_{\normalsize 0} \normalsize (1)du=0.95
계산하면 a = 0.95. 따라서,
P(U \leq 0.95)=P(\dfrac{Y}{\theta} \leq 0.95)=P(Y \leq 0.95 \theta) = P(\dfrac{Y}{0.95} \leq \theta) = 0.95
Y/0.95 가 0.95 신뢰계수를 갖는 θ에 대한 하한신뢰한계이다. 관측값 Y 가 θ 보다 항상 작기 때문에, 하한신뢰한계가 Y 값 보다 살짝 더 큰 값을 가져야 한다는 점이 직관적으로도 타당해 보인다.
위에서 살펴본 두 예제들은 미지의(unknown) 파라미터들의 신뢰한계 값을 찾는 피보탈 방식을 보여주고 있다. 각각의 경우에 구간 추정치들은 분포상의 단일 관측값에 기반하여 얻어졌다. 이 예제들은 일단 이 방식을 보다 쉽게 설명하는데 목적이 있었고 향후 포스트들에서는 좀 더 실제적인 중요성을 갖는 구간추정 방식을 살펴보기 위해 표본 분포와 피보탈 방식을 결합한 방식을 살펴보도록 하겠다. (이 방식이 흔히 더 잘 알려져 있다.)
