가설검정 (Hypothesis Testing) – 다(多) 표본 검정

 

 

 

 

 

이번 포스트는 가설검정의 두번째 포스트로 다(多) 표본 검정 (Common Large-Sample Tests)을 다룬다. 내용은『Mathematical Statistics with Applications, Sixth Edition, DUXBURY , Dennis D. Wackerly / William Mendenhall / Richard L. Scheaffer』 를 참고했다.

2. 다 표본 검정 (Common Large-Sample Tests)

랜덤 표본 Y_1, Y_2,\cdots, Y_n 에 기초하여 파라미터  \theta 에 대한 가설들을 테스트하고자 한다고 가정하자.

이번 포스트에서는 평균  \theta 와 표준편차  \sigma_{\hat{\theta}} 의 정규분포를 (근사적으로) 따르는 추정량 \hat{\theta} 에 기초한 가설검정을 다룬다. 이미 점 추정(Point Estimation) 에서  \bar{Y} 나  \hat{p} 등이 평균 \mu 과 비율 p 에 대한 추정량으로 사용되는 것을 지켜봤다. (이전 포스트 참조)  (\mu_1 - \mu_2) 나  (p_1 - p_2) 에 대해서도 마찬가지다.

 

만약 \theta_0 가  \theta 에 대한 특정 값이라고 할 때, 우리는 귀무가설 H_0 : \theta = \theta_0 와 대립가설 H_a : \theta > \theta_0 를 테스트하고 싶다. 아래 그림은 모 파라미터  \theta 에 대한 다양한  \hat{\theta} 값들의 표본분포 (sampling distribution) 을 나타내고 있다.

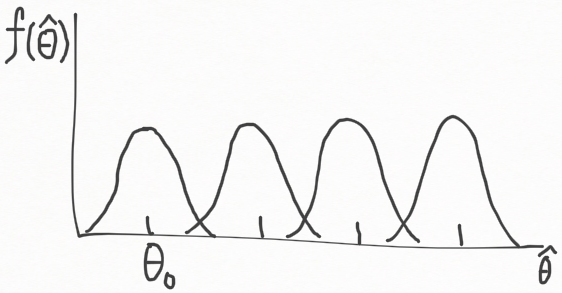
만약  \hat{\theta} 이  \theta_0 에 가깝다면 귀무가설 H₀ 를 채택하는게 타당하다. 그러나 만약 실제는 \theta > \theta_0 라면,  \hat{\theta} 은 더 큰 값일 것이다. 마찬가지로  \hat{\theta} 가  \theta_0 에 비해 큰 값이라면, 귀무가설  H_0 : \theta = \theta_0 을 기각하고 대립가설  H_a : \theta > \theta_0 을 채택하는게 맞다. 대립가설, 귀무가설, 검정 통계량, 기각역은 다음과 같다.

H0 : \theta = \theta_0 Ha : \theta > \theta_0 Test Statistic : \hat{\theta} Rejection Region : RR = \{\hat{\theta}>k\} for some choice of k

기각역 RR 안에 속하는 실제 k 값은 type Ⅰ error 의 확률 α 를 확정하면 결정된다. ( α 는 검정 수준 혹은 레벨 이라고 지칭한다. ) 만약 귀무가설 H₀ 가 참이면,  \hat{\theta} 은 평균  \theta_0 와 표준편차  \sigma_{\hat{\theta}} 인 정규분포를 근사적으로 따른다. 그러므로,  α-level test

k = \theta_0 + z_{\alpha}\sigma_{\hat{\theta}}

 

는 적절한 k 값을 찾는 것이 된다. [ 만약 Z 가 표준정규분포를 따르면 [z_α 는 P(Z>z_{\alpha}) = \alpha 를 만족한다. ]

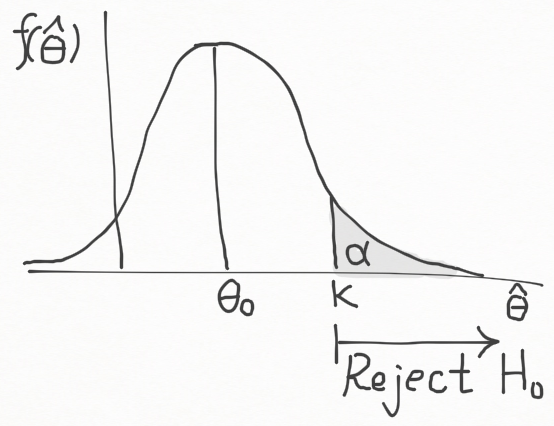
왜냐하면 Z = (\hat{\theta}-\theta_0) / {\sigma_{\hat{\theta}}} 를 검정 통계량으로 사용하면,

RR = \{\hat{\theta}:\hat{\theta}>\theta_0+z_{\alpha}\sigma_{\hat{\theta}}\} =\{\hat{\theta}:\dfrac{\hat{\theta}-\theta_0}{\sigma_{\hat{\theta}}}>z_{\alpha}\}

 

기각역은 RR=\{z > z_{\alpha}\} 로 쓸수 있다. 여기서 Z 는 귀무가설을 만족하는  \theta 값에 대해  \theta 의 추정량과 \theta_0 사이의 표준 오차를 측정한다. 따라서 동일한 형태의 가설 검정식은 다음과 같다.

H0 : \theta = \theta_0 Ha : \theta > \theta_0 Test Statistic : Z=\dfrac{\hat{\theta}-\theta_0}{\sigma_{\hat{\theta}}} Rejection Region : \{z>z_{\alpha}\}

만약 Z 값이 커서 표준정규분포의 upper-tail (오른쪽 꼬리) 에 위치한다면 귀무가설  H_0 : \theta = \theta_0 를 기각한다. 대립가설  H_a : \theta > \theta_0 는 upper-tail 대립가설, RR =  \{z>z_{\alpha}\} 는 upper-tail 기각역이라고 부른다. 앞선 공식의 Z 는

Z = \dfrac{estimator~for~the~parameter~-~value~for~the~parameter~given~by~H_0}{standard~error~of~the~estimator}

 

라고 할 수 있다.

 

예제1. 어느 대기업 영업담당 부사장은 영업사원들이 평균적으로 한 주에 15건 이하의 영업실적을 올린다고 주장한다. (더 많은 영업량 달성을 독려하기 위해) 표본 n = 36 의 영업사원들의 영업실적을 확인해 본 바, 그 평균과 분산은 17, 9 였다. (영업실적은 특정 주간의 랜덤하게 선택된 영업사원들에 의해 기록되었다.) 그 관측결과가 부사장의 주장을 뒤엎을 수 있는 증거가 될 것인가? α = 0.05 를 사용하여 검증하라.

풀이.

우리가 하려는 건 부사장의 주장이 틀렸다는 것을 검증하는데에 있다. 즉 H_a : \mu > 15 이며, μ 는 주당 영업사원 1명의 실적 평균이다. 따라서

H_0 : \mu = 15

 

H_a : \mu > 15

 

을 검정하면 된다. n 이 큰 경우에 \bar{Y} 는 μ 에 대한 점 추정량이 되며, 근사적으로 \mu_{\bar{Y}}=\mu 이고 \sigma_{\bar{Y}}=\sigma/\sqrt{n} 인 정규분포를 따른다. 따라서 검정 통계량은

Z =\dfrac{\bar{Y}-\mu_0}{\sigma_{\bar{Y}}}=\dfrac{\bar{Y}-\mu_0}{\sigma/\sqrt{n}}

 

이 된다. α = 0.05 인 기각역은 \{z>z_{0.05}=1.645\} 로 주어진다. 모 분산인 \sigma^2 는 알지못하지만, 비교적 정확하게 (n = 36 이므로) s^2=9 으로 추정할 수 있다. 검정 통계량의 관측된 결과는,

z =\dfrac{\bar{y}-\mu}{s/\sqrt{n}}=\dfrac{17-15}{3/\sqrt{36}}=4

 

Z 의 관측된 결과가 기각역에 속하므로 ( 4 > z_0.05 = 1.645 ), 귀무가설  H_0 : \mu = 15 을 기각한다.  따라서 α = 0.05 인 유의수준 (level of significance) 에서는 부사장의 주장이 틀렸다는 증거가 충분하며, 한 주간 영업사원의 평균 실적은 15건을 초과한다고 할 수 있다.

 

예제2. 어떤 제조공장의 기계에서 생산된 제품이 하루에 10% 이상의 불량율이 발견된다면 반드시 수리를 해야 한다고 하자. 100개 제품을 랜덤하게 표본으로 뽑아서 15개의 불량이 발견되었다고 한다. 현장 관리자는 기계를 반드시 수리해야 한다고 했다. 관측된 결과가 그의 주장을 뒷받침 할 수 있는가? 테스트 수준 0.01 로 검증하라.

풀이.

Y 를 관측된 불량의 수라고 하자. Y 는 이항분포를 따르며 이 때 확률 p 는 랜덤하게 선택된 제품이 불량일 확률이다. 우리가 테스트해야 하는 것은

H₀ : p =0.10

Ha : p > 0.10

이다. 검정 통계량은 \hat{p} = Y/n (unbiased estimator of p) 일때,

Z =\dfrac{\hat{p}-p_0}{\sigma_{\hat{p}}}=\dfrac{\hat{p}-p_0}{\sqrt{\dfrac{p_0(1-p_0)}{n}}}

 

으로 주어진다. 여기서는  \hat{p} 의 근사치로 \sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}} 를 사용해야 하지만 H₀ 일 때 Z 의 분포를 고려하여  H₀ 가 사실일 때 \hat{p} 의 표준오차의 실제값인 \sqrt{\dfrac{p_0(1-p_0)}{n}} 를 사용했다. P(Z > 2.33) = 0.01 이므로, {z>2.33} 을 기각역으로 채택할 수 있다.

검정통계량의 관측된 결과는,

z =\dfrac{\hat{p}-p_0}{\sqrt{\dfrac{p_0(1-p_0)}{n}}} =\dfrac{0.15-0.10}{\sqrt{\dfrac{(0.1)(0.9)}{100}}}=\dfrac{5}{3}=1.667

 

Z가 기각역에 속하지 않기 때문에 귀무가설 H₀ : p =0.10 를 기각할 수 없고, 대립가설 Ha : p > 0.10 을 채택해야 한다. 즉, α = 0.01 유의수준에서 현장 관리자의 결정은 증거가 불충분하다고 결론 내릴 수 있다.

그렇다면 관리자가 틀린것인가? 대립가설 Ha 가 사실일 때, H₀ 를 채택할 확률을 검증할 때까지는 통계적인 결정을 쉽게 내릴 수 없다. 이것을 type Ⅱ error (β) 라고 하고 다음 포스트에서 다루기로 하자.

 

다음으로 다른 형태의 대립가설에 대한 가설검정을 좀 더 살펴보도록 하자.

H₀ : \theta = \theta_0

Ha : \theta < \theta_0

 

유사하게 검정할 수 있다. 검정 통계량은 동일하게,

Z=\dfrac{\hat{\theta}-\theta_0}{\sigma_{\hat{\theta}}}

 

이 된다. 하지만 기각역은  \{z<-z_{\alpha}\} 가 된다. 표준정규분포 상에서 왼쪽 꼬리 영역에 기각역이 위치하기 때문이다. Ha : \theta < \theta_0 를 lower-tail (왼쪽 꼬리) 대립가설이라고 하고, 기각역 RR : \{z<z_{\alpha}\} 를 lower-tail 기각역이라고 한다.

 

한편,

H₀ : \theta = \theta_0

Ha : \theta \not= \theta_0

 

인 경우는 귀무가설 H₀ 를 \hat{\theta} 가 \theta_0 에 비해 매우 작거나 큰 경우 기각할 수 있다. 검정 통계량은 Z로 같지만, 기각역은 Z 의 분포의 양쪽 꼬리영역에 대칭적으로 위치한다. 따라서 H₀ 를 기각할 때는 z < -z_{\alpha/2} 또는  z > z_{\alpha/2} 일 때 이다. 간단하게 |z| > z_{\alpha/2} 라고 할 수 있다. 이것을 \theta < \theta_0 이거나  \theta > \theta_0 인 one-tailed test (단측 검정) 과 구분하여 two-tailed test (양측 검정) 이라고 한다. Ha : \theta < \theta_0 인 lower-tail 대립가설과 Ha : \theta \not= \theta_0 인 two-sided 대립가설의 기각역을 아래 그림에 표시하였다.

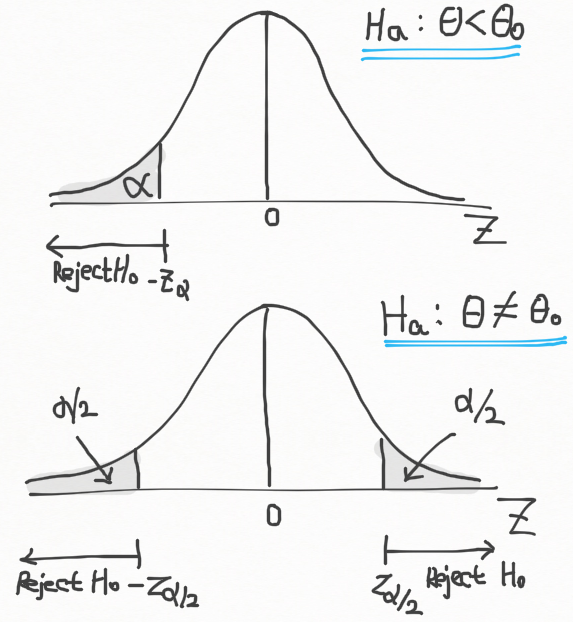
α-유의수준의 다(多) 표본 (large-sample) 가설검정에 대해서 지금까지 다룬 것들을 아래에 정리하였다.

α-유의수준의 다(多) 표본 (large-sample) 가설검정 H0 : \theta = \theta_0 Ha : \theta > \theta_0 (upper-tail alternative) \theta < \theta_0 (lower-tail alternative) \theta \not= \theta_0 (two-tailed alternative) 검정 통계량 :  Z = \dfrac{\hat{\theta}-\theta_0}{\sigma_{\hat{\theta}}} 기각역 : \{z>z_{\alpha}\} (upper-tail RR) \{z<-z_{\alpha}\} (lower-tail RR) \{|z|>z_{\alpha/2}\} (two-tailed RR)

어떤 test 를 수행해야 하는가는 어떤 것을 검증하려 하는가에 달려 있다.

 

예제3. 자극의 반응에 대한 남성과 여성의 반응 시간에 대한 심리조사가 수행되었다. 독립적인 랜덤표본으로 남성 50명과 여성 50명을 선발하였다. 조사 결과가 다음과 같을 때 남성과 여성의 실제 반응시간에 차이가 있는가에 대해 검증하라. (α = 0.05) 남성 여성 n_1 = 50 \bar{y_1}=3.6 seconds s^2_1 = 0.18 n_2= 50 \bar{y_2}=3.8 seconds s^2_2 = 0.14

\mu_1 과  \mu_2 를 남성과 여성의 실제 반응시간이라고 하자. 가설검증은 두 모평균이 차이가 난다는 것을 검증하는 것이므로, 귀무가설 H₀ : (\mu_1 - \mu_2) =0 에 대해 대립가설 Ha : (\mu_1 - \mu_2) \not= 0 를 수립할 수 있다. two-tailed test (양측 검정) 을 수행하여  \mu_1 > \mu_2 이거나  \mu_1 < \mu_2 를 보이면 귀무가설을 기각할 수 있다.  (\mu_1 - \mu_2) 에 대한 점 추정량은  (\bar{Y_1}-\bar{Y_2}) 이다. H₀ : \mu_1 - \mu_2=D_0 를 검정하려고 하면, 검정 통계량은 다음과 같이 설정하면 된다.

Z = \dfrac{(\bar{Y_1}-\bar{Y_2})-D_0}{\sqrt{\dfrac{\sigma_1^2}{n_1}+\dfrac{\sigma_2^2}{n_2}}}

 

이 경우 two-tailed test 를 수행해야 하므로 α = 0.05 이므로, 기각역은 |z| > z_{\alpha/2}=z_{0.025}=1.96 이 된다. n이 충분히 크므로 ( n > 30 ) 표본분산이 모 분산  \sigma_1^2 , \sigma_2^2 의 훌륭한 추정량이 된다. \bar{Y_1},\bar{Y_2}, n_1, n_2, D_0=0 를 찾아서 대입하면,

z =\dfrac{(\bar{y_1}-\bar{y_2})-0}{\sqrt{\dfrac{\sigma_1^2}{n_1}+\dfrac{\sigma_2^2}{n_2}}}\approx\dfrac{3.6-3.8}{\sqrt{\dfrac{0.18}{50}+\dfrac{0.14}{50}}}=-2.5

 

이 값은 -z_{/alpha/2}=-1.96 보다 작다. 따라서 기각역에 속하므로 유의수준 (α) = 0.05 에 대해 남성과 여성의 반응시간은 다르다는데 충분한 증거가 된다고 말할 수 있다.

 

Series Navigation

<< 가설검정 (Hypothesis Testing) – 통계적 검정의 요소가설검정 (Hypothesis Testing) – Type Ⅱ Error 확률 계산과 Z-Test Sample Size 찾기 >>